ARTÍCULOS
"Los negros no son buenos para las matemáticas": Ideologías raciales y prácticas de enseñanza de las matemáticas en Colombia**
"Blacks aren't good for math": Racial ideologies and mathematics teaching practices in Colombia
"Os negros não são bons em matemática": Ideologias raciais e práticas de ensino da matemática na Colômbia
LUZ EDITH VALOYES CHÁVEZ*
* Profesora de la Facultad de Educación de la Universidad Santiago de Cali, Cali, Colombia. Licenciada en Matemática y Física de la Universidad del Valle con maestría en Educación con énfasis en Educación Matemática de la misma Universidad y doctorado de la Universidad de Missouri en los Estados Unidos. En 2010 obtuvo una beca Fulbright para líderes Afrodescendientes. Ha participado como investigadora en diversos proyectos relacionados con el aprendizaje y la enseñanza del álgebra. Sus intereses de investigación se relacionan con problemáticas de poder y educación matemáticas, formación de maestros de matemáticas, e ideologías raciales y prácticas de enseñanza de las matemáticas. Correo electrónico: luz.valoyes00@usc.edu.co, evaloyes@gmail.co
Recibido: 23/02/2015
Aceptado: 07/07/2015
RESUMEN
El estudio explora las formas en la que las identidades raciales de los estudiantes nutren las expectativas de los maestros y configuran las prácticas de enseñanza del álgebra. Usando el método comparativo y un enfoque interpretativo, se analizaron las ideologías raciales y las prácticas de enseñanza de tres maestros de matemáticas en diferentes contextos sociales, culturales y raciales en Cali. Los resultados indican la presencia en la escuela de ideologías sobre los estudiantes negros que los posicionan como incapaces de aprender matemáticas. Estas ideologías se traducen en prácticas de enseñanza e interacciones pobres que podrían explicar su bajo desempeño en matemáticas. Se discuten algunas implicaciones para la investigación y la formación de maestros.
Palabras clave: Ideologías raciales; álgebra; enseñanza de las matemáticas; racismo.
ABSTRACT
The study focuses on the forms wherein student racial identities nurture and shape teacher expectations and influence the teaching practices of algebra. Using a comparative method and an interpretative approach, racial ideologies and teaching practices of three different mathematics teachers in three different social, cultural and racial contexts in Cali, Colombia were studied. The findings highlight the prevalence of cultural and class deficit views about black students that position them as incapable of learning mathematics. These racial ideologies translate into poor teaching practices and interactions that could explain their low mathematics performance. Implications for research and teacher education are suggested.
Key words: Racial ideologies; algebra; mathematics; teaching practices; racism.
RESUMO
O estudo explora as formas na que as identidades raciais dos estudantes nutrem as expectativas dos professores e configuram as práticas de ensino da álgebra. Usando o método comparativo e um enfoque interpretativo, se analisaram as ideologias raciais e as práticas de ensino de três professores de matemática em diferentes contextos sociais, culturais e raciais em Cali. Os resultados indicam a presença na escola de ideologias sobre os estudantes negros que os posicionam como incapazes de aprender matemática. Estas ideologias se traduzem em práticas de ensino e interações pobres que poderiam explicar o seu baixo desempenho em matemática. Discutem–se algumas implicações para a pesquisa e a formação de professores.
Palavras chave: Ideologias raciais; álgebra; ensino da matemática; racismo
Introducción
Diferentes autores han señalado las dificultades que surgen al intentar estudiar fenómenos relacionados con el racismo en los sistemas educativos (DIME, 2007; Parks y Schmeichel, 2012; Reyes y Stanic, 1988). En primer lugar, limitaciones de orden teórico y metodológico dificultan desentrañar y visibilizar las prácticas educativas a través de las cuales los estudiantes negros son discriminados en la escuela. Adicionalmente, las ideologías del mestizaje, la democracia racial y de la meritocracia –fuertemente arraigadas en las sociedades actuales– expresan el escepticismo de investigadores y de la sociedad en general en relación con la existencia de discriminación racial en la escuela. Dicho escepticismo emerge como un obstáculo para adelantar procesos investigativos que visibilicen y permitan hablar abiertamente de las prácticas que excluyen y marginalizan a estudiantes negros en los sistemas educativos y que restringen su derecho a educación de calidad.
Lo anterior es particularmente notable en la educación matemática. Históricamente, la investigación en este campo científico se ha centrado en el estudio de los fenómenos que surgen durante los procesos de comunicación del saber matemático desde perspectivas eminentemente cognitivas. Desde estas perspectivas, el impacto en los procesos de construcción del saber matemático de las identidades raciales, étnicas, de género y de clase de los maestros y los estudiantes, y sus actos de posicionamiento en el salón de clase no son aspectos relevantes para comprender las diferencias en resultados de aprendizaje, en las experiencias escolares de los estudiantes y en el acceso desigual a educación matemática de calidad. Aunque desde enfoques socioculturales y antropológicos se han abordado problemáticas concernientes con diferencias en el logro educativo y en las experiencias de aprendizaje de las matemáticas con base en el género y la clase (Baird, 2012; Bolaer, 2002; Borman y Overman, 2004), cuestiones relacionadas con las formas en las cuales procesos de exclusión y marginalización por raza tienen lugar y se manifiestan en la clase de matemáticas han sido escasamente abordadas (DIME, 2007). Así, aunque la investigación dominante en el campo ha contribuido sustancialmente a la consolidación de la educación matemática como una disciplina científica, es también evidente que este tipo de investigación es limitada en cuanto a sus posibilidades de análisis y explicación de las inequidades raciales –entre otras– en el aprendizaje y la enseñanza de las matemáticas. Cuando tienen lugar, tanto la investigación como los discursos sobre raza y racismo en la educación matemática son sistemáticamente marginalizados. Un paso fundamental en la consolidación del campo es cuestionar los paradigmas que orientan las prácticas investigativas, de tal manera que problemáticas raciales y otras relacionadas con poder, equidad y justicia social puedan abordarse plenamente.
Este artículo aborda la problemática de la exclusión y marginalización de los estudiantes negros durante los procesos de enseñanza y aprendizaje de las matemáticas. Mis principales propósitos son, en primer lugar, contribuir a visibilizar problemáticas de racismo y discriminación racial en el campo de la educación matemática en Colombia; en segundo lugar, me propongo avanzar en la elaboración de constructos teóricos y metodológicos que nos permitan comprender mejor las experiencias escolares de los estudiantes negros y sus procesos de construcción de identidad matemática (Martin, 2006; Nasir, 2002). Para lograr estos propósitos, y con base en constructos tomados de la sociología (Bonilla–Silva, 2006; 2010; Giroux, 1981; Williams, 1981), analizo las ideologías raciales y la naturaleza de las interrelaciones que tienen lugar durante los procesos de construcción del saber matemático en los salones de clase de tres maestros de matemáticas en la ciudad de Cali. En particular, intento dar respuesta a las siguientes preguntas:
¿De qué manera maestros de matemáticas de grado octavo explican y/o justifican los resultados de aprendizaje de los estudiantes negros en sus salones de clase?
¿Cuál es la forma que toman las relaciones entre los maestros y los estudiantes a lo largo de líneas raciales durante los procesos de construcción del saber matemático?
La selección de los grados octavos como foco del presente estudio responde al papel central que tiene el álgebra en el currículo colombiano. A partir de grado octavo, las matemáticas escolares aparecen altamente algebrizadas (Valoyes, 2013) y en adelante, será muy difícil para los estudiantes acceder a la geometría analítica, la trigonometría y el cálculo sin una buena fundamentación del saber algebraico. Como consecuencia, el fracaso en el aprendizaje del álgebra representa un obstáculo para que los estudiantes puedan continuar y culminar con éxito sus estudios secundarios y para que potencialmente puedan acceder a la universidad. Adicionalmente, la alfabetización algebraica es considerada por algunos investigadores (e.g., Moses y Cobb, 2001) como fundamental para la participación en la vida política y democrática de las sociedades en tanto que decisiones que afectan la vida de las personas se toman con base en modelos algebraicos.
Mi interés en problemáticas relacionadas con la educación matemática de los estudiantes negros tiene su origen en mis propias experiencias, como mujer negra que ha tratado de navegar exitosamente a través del sistema educativo colombiano. Durante mi proceso de formación básica enfrenté el escepticismo de algunos maestros, quienes muchas veces expresaban su sorpresa al encontrar una estudiante negra y "buena" para las matemáticas. Adicionalmente, mi interés en estas problemáticas tiene sus raíces en mi participación en un proyecto de investigación acerca de las expectativas de los maestros en relación al aprendizaje de las matemáticas de estudiantes de minorías raciales y étnicas en los Estados Unidos durante mis estudios de doctorado. Dicha experiencia me permitió constatar y confirmar el carácter político de los prácticas de aprendizaje y enseñanza de las matemáticas y la importancia de abordar dichas problemáticas en un país como Colombia, con fuertes problemas de inequidad y exclusión social (Programa de las Naciones Unidas para el Desarrollo [PNUD], 2011).
En la primera parte de este artículo, presento un panorama de los resultados de aprendizaje de los estudiantes negros en Colombia –y particularmente en Cali– con base en los puntajes de las pruebas Saber 9. En la segunda parte discuto la forma como se ha abordado la problemática racial en el campo de la educación matemática. En la tercera, describo la metodología utilizada para adelantar el estudio que presento. Finalmente describo los resultados y las conclusiones.
Un panorama de la formación matemática de los estudiantes negros en Colombia
En contraste con el escenario internacional, donde diversos estudios han analizado el desempeño matemático de los estudiantes negros en los sistemas educativos (Lee, 2002; Lubienski, 2002; Ogbu, 1988; Riegle–Crumb y Grodsky, 2010; Tate, 1997), en Colombia las diferencias en los resultados de aprendizaje de los estudiantes colombianos generalmente se analizan con base en la clase o el género (Instituto Colombiano para el Fomento de la Educación Superior [ICFES], 2009; 2010; García, Espinosa, Jiménez, y Parra, 2013) ignorándose completamente la variable racial. Como resultado, no existe información detallada y confiable acerca del desempeño matemático de los estudiantes negros en el país.
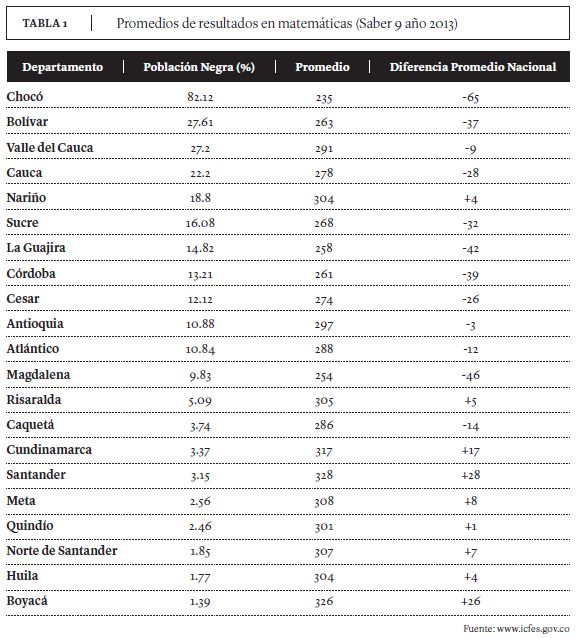
De acuerdo con los resultados de las pruebas Saber 9 aplicadas en el año 2013, los niños, los estudiantes de estratos socioeconómicos altos y los que atienden escuelas privadas o ubicadas en las zonas urbanas obtienen mejores resultados en el aprendizaje de las matemáticas. Dado que en la encuesta sociodemográfica que aplica el ICFES a los estudiantes que presentan las pruebas Saber no se incluye la variable racial, una forma de caracterizar el desempeño matemático de los estudiantes negros es a través del análisis de los resultados por regiones y/o departamentos tomando como base su composición racial. Así, al analizar los resultados de las prueba en el año 2013, se encuentra que los departamentos cuyos promedios en matemáticas se ubican significativamente por debajo del promedio nacional son aquellos localizados sobre las costas Pacífica y Atlántica en donde se concentra el mayor porcentaje de población negra en el país. La tabla 1 resume estos resultados.
Chocó, el departamento con el mayor porcentaje de población negra, es también el más afectado por el bajo nivel de desempeño de los estudiantes en matemáticas. La diferencia entre su promedio y el del país es de 65 puntos, superando ampliamente las diferencias de los demás departamentos. Este situación se repite en los departamentos de Magdalena, Bolívar, Cauca, Córdoba, Guajira, Sucre y Cesar, cuyos porcentajes de población negra superan el promedio nacional. En contraste, los departamentos ubicados en la región andina, cuyo porcentaje de población negra se ubica por debajo del promedio nacional, muestran resultados de aprendizaje significativamente mejores y muy por encima del promedio nacional.
Los departamentos del Valle, Antioquia y Nariño parecieran ser excepciones a la relación entre el porcentaje de población negra y el bajo nivel de desempeño en matemáticas (ver Tabla 1). El promedio en las pruebas de los estudiantes en Nariño, cuyo porcentaje de población negra es cercano al 20%, es cuatro puntos más alto que el promedio nacional. Aunque podría considerarse que esta no es una diferencia significativa, es importante resaltar que cuando se analizan en detalle los puntajes de los municipios del departamento, los resultados son reveladores en cuanto a la relación entre raza y logro educativo en matemáticas.
La tabla 2 muestra que los municipios cuya población es mayoritariamente negra obtienen promedios muy por debajo del promedio departamental, mientras que aquellos cuya composición racial es mayoritariamente mestiza obtienen promedios por encima del promedio del departamento. Así pues, se revela una tendencia a nivel nacional y departamental, según la cual el fracaso escolar en matemáticas parece concentrarse fundamentalmente en los departamentos y municipios habitados principalmente por comunidades negras.
Consideremos el caso de Cali, la ciudad en la que se adelantó el estudio. Como una expresión de la segregación racial que experimenta la ciudad, la población negra se concentra en las comunas 7 (37%), 13 (38%), 14 (51%), 15 (41%) y 21 (45%) en el oriente de la ciudad; estas comunas y la 20 son también las más pobres. Los resultados de las pruebas Saber que analizamos muestran que la mayoría de los estudiantes caleños se ubican en los niveles de desempeño insuficiente (20%) y mínimo (56%) y que sólo una minoría alcanza desempeños en los niveles superior (20%) y avanzado (3%). Se podría entonces concluir que el bajo desempeño en matemáticas afecta a la mayoría de los estudiantes en la ciudad. Sin embargo, cuando estos resultados se desagregan por comunas, es posible identificar una relación importante entre el nivel de logro en matemáticas y la composición racial de las comunas. La figura 1 muestra dos hechos importantes. En primer lugar, se evidencia que las comunas más afectadas por el bajo desempeño en matemáticas son también –con excepción de la comuna 20– aquellas cuya población negra se encuentra por encima del promedio de la ciudad. La cantidad de estudiantes ubicados en el nivel insuficiente es mayor en estas comunas en comparación con el resto de la ciudad. En la comuna 21, por ejemplo, más de la mitad de los estudiantes se ubica en el nivel de desempeño matemático más bajo, indicando que los estudiantes ni desarrollaron los procesos de pensamiento matemático esperados para el grado noveno ni demuestran los desempeños mínimos establecidos. Estos resultados en Cali confirman la tendencia, anteriormente visibilizada a nivel nacional, a que el fracaso escolar en matemáticas se concentre principalmente y de manera significativa en los lugares con mayor presencia de población negra.
Aunque no se puede desconocer el efecto de factores tales como la pobreza y la violencia en los resultados de aprendizaje en matemáticas en estos departamentos, municipios y comunas, es posible señalar esta tendencia en que se intersectan la raza y el logro escolar en matemáticas. De acuerdo con ella, el fracaso escolar en esta disciplina estaría afectando mayoritariamente a los estudiantes negros en Colombia, con las consecuencias para su movilidad social y participación en la vida social y democrática que esto genera. Luego, para entender las experiencias educativas de los estudiantes negros y los resultados de aprendizaje de las matemáticas, es necesario tener en cuenta las formas en las cuales la raza emerge en la clase de matemáticas en el sistema educativo colombiano para condicionar las interrelaciones entre maestros y estudiantes y las prácticas de enseñanza y de aprendizaje de esta disciplina.
Raza, racismo y educación matemática
Estudio de la raza y el racismo en el campo de la educación matemática
Generalmente los estudios que analizan diferencias en el logro escolar en matemáticas consideran la raza exclusivamente como una variable demográfica o categoría estadística que permite clasificar el desempeño de los estudiantes con base en puntajes obtenidos en pruebas estandarizadas nacionales e internacionales (Ladson–Billings y Tate, 1995). Desde estas perspectivas la raza es asumida como un constructo políticamente neutro dentro de los procesos de investigación en el campo y como un elemento cuya función principal consiste en facilitar el establecimiento de categorías de desempeño matemático.
Martin (2009) sostiene que esta manera de abordar la raza en los procesos de investigación ha contribuido a la naturalización del fracaso escolar en matemáticas de los negros y a la creación de una estratificación racial de las habilidades matemáticas entre grupos de estudiantes. De acuerdo con dicha estratificación, los estudiantes blanco–mestizos serían más hábiles en matemáticas y contarían naturalmente con las capacidades y disposiciones para aprender esta disciplina; lo anterior en abierto contraste con los estudiantes negros, quienes carecerían de dichas condiciones para el aprendizaje exitoso de las matemáticas. En este sentido, su fracaso en el aprendizaje de las matemáticas es esperado y el bajo número de estudiantes negros aceptados en programas con una fuerte fundamentación matemática como las ingenierías o la administración de negocios es un hecho visto como consecuencia natural de la ausencia de habilidades matemáticas entre esta población estudiantil.
Las diferencias en los desempeños en matemáticas entre distintos grupos de estudiantes son generalmente explicadas y justificadas apelando a discursos esencialistas (Boaler, 2002). De acuerdo con dichos discursos, el origen de estas diferencias se encuentra en la diversidad cultural o en las identidades raciales, de género o de clase de los estudiantes. Dado que existe una jerarquía de habilidades matemáticas y una predisposición natural de ciertos grupos humanos para el aprendizaje exitoso de esta disciplina, es poco lo que pueden hacer los gobiernos o las instituciones educativas para mejorar las condiciones en las cuales minorías raciales aprenden y construyen identidades matemáticas positivas. En este sentido, los discursos esencialistas, además de naturalizar el fracaso escolar de grupos determinados de estudiantes, liberan de la responsabilidad de dicho fracaso tanto al gobierno como a las instituciones educativas y contribuyen a minimizar y ocultar el papel de las prácticas de enseñanza de las matemáticas en la configuración de los resultados de aprendizaje de las matemáticas y de la experiencias escolares de los estudiantes. Los discursos esencialistas desvían la atención del racismo en la escuela y contribuyen de manera fundamental a encubrir prácticas de exclusión y marginalización durante los procesos de enseñanza y aprendizaje que podrían explicar el fracaso escolar en matemáticas de los estudiantes negros e indígenas, entre otros.
En contraste con esta aproximación a la noción de raza y como una manera de confrontar discursos esencialistas, en los últimos años, investigadores en educación matemática apoyados fundamentalmente en desarrollos de la sociología han empezado a reelaborar la forma como dicha noción se utiliza y se define en los procesos de investigación en el campo. Desde estas perspectivas se considera la raza fundamentalmente como un constructo social, históricamente contingente y sujeto a resistencia, contestación y negociación (Martin, 2009).
De acuerdo con Bonilla–Silva (2010), la raza tiene efectos reales sobre la vida de las personas: el acceso a los espacios de poder en la sociedad queda condicionado a su ubicación en la jerarquía racial que resulta de este proceso de racialización. En otras palabras, el acceso de las personas a la educación, la salud, la vivienda, al trabajo digno y a su participación política, es condicionado por su posición en la estructura racial de la sociedad.
La investigación desarrollada en esta perspectiva ha permitido identificar diferentes factores que influyen en los resultados de aprendizaje y que condicionan las experiencias escolares de los estudiantes negros durante los proceso de construcción del saber matemático. En primer lugar, algunos estudios han identificado factores estructurales que contribuyen al fracaso escolar en matemáticas de los estudiantes negros. Entre tales factores se encuentra la insuficiente preparación de los maestros para enseñar matemáticas a poblaciones estudiantiles diversas (Zevenbergen, 2003), la organización escolar inadecuada para atender y responder a las necesidades educativas de dichas poblaciones y una pobre financiación de las escuelas atendidas especialmente por estudiantes negros (Darling–Hammond, 2004). En segundo lugar, han sido identificados elementos y condiciones que favorecen el aprendizaje exitoso de las matemáticas y la construcción de identidades matemáticas positivas por parte de estudiantes negros (Berry 2008; Nasir y Hand, 2006; Walker, 2006). Adicionalmente, desde estas nuevas aproximaciones a la noción de raza ha sido posible determinar prácticas de enseñanza que podrían explicar los resultados de aprendizaje de los estudiantes negros, tales como el énfasis en la memorización de procedimientos rutinarios y de conocimientos matemáticos básicos (Hoadley, 2007; Oakes, 2005), así como la ausencia de experiencias de aprendizaje que permitan el desarrollo de procesos de pensamiento matemático complejo como el razonamiento, la comunicación y la solución de problemas (Lee, Smith y Croninger, 1997). Aunque en el panorama internacional se evidencia un esfuerzo importante por estudiar y comprender las experiencias de los estudiantes negros durante los procesos de construcción y comunicación del saber matemático, también es cierto que estos esfuerzos son inexistentes en el contexto colombiano.
Estructuras e ideologías raciales en la educación matemática
Para entender la forma como el racismo opera durante los procesos de enseñanza y aprendizaje de las matemáticas, es necesario develar los mecanismos y las prácticas que reproducen la dominación racial durante dichos procesos. En otras palabras, es importante comprender la forma como la discriminación racial funciona, opera y se institucionaliza en la clase de matemáticas. De acuerdo con Bonilla–Silva (2010), las estructuras raciales en las sociedades consisten en redes de interacciones y de prácticas entre los grupos humanos basadas en distinciones raciales. Dichas interacciones y prácticas son guiadas por ideologías raciales las cuales se expresan a través de los discursos (Van Dijk, 1992) que median tanto las interacciones como las prácticas y que les permiten a las personas naturalizar, explicar y justificar las inequidades raciales en las distintas instituciones que constituyen la sociedad. Es importante en este punto anotar que, aunque las ideologías raciales se expresan fundamentalmente en forma discursiva, no es posible reducirlas solamente a discursos o ideas que habitan en la mente de las personas en tanto que ellas contribuyen a la reproducción de prácticas en las diferentes instituciones sociales. Obviamente, no pretendo agotar o reducir la complejidad de la relación entre ideología y práctica a estas afirmaciones. Por el contrario, este estudio es un intento de develar una de las aristas de dicha relación en el caso de las ideologías raciales y las prácticas de enseñanza de las matemáticas.
Asumo entonces que la escuela, como institución fundamental del desarrollo, reconfiguración y mantenimiento de las estructuras sociales, no es ajena a interrelaciones y prácticas basadas en la raza. Por el contrario, ella es parcialmente estructurada por la ubicación de los actores educativos en categorías raciales que determinan prácticas, relaciones y discursos y, de esta manera, acceso diferenciado a educación de calidad. Así pues, la escuela no es un espacio neutro en relación con problemáticas de racismo; en ella se expresan agudas tensiones raciales que deben ser analizadas para comprender las experiencias escolares de los estudiantes de minorías raciales –en particular de los estudiantes negros–. Son justamente estos elementos los que evidencian los estudios mencionados en el apartado previo.
Adicionalmente reconozco el carácter situado, político e histórico de la educación matemática. Para entender los fenómenos que se presentan durante la construcción del saber matemático es necesario reconocer que los procesos de enseñanza y aprendizaje de las matemáticas no son sólo cognitivos o socioculturales, sino que son de naturaleza política. Ellos no ocurren al margen de dinámicas y tensiones sociales, raciales, políticas o económicas que tienen lugar en las sociedades actuales. Las prácticas de enseñanza y aprendizaje de las matemáticas contribuyen de manera fundamental a la reproducción y sostenimiento de inequidades en la sociedad debido, particularmente, al papel fundamental que juega esta disciplina en el desarrollo tecnológico y económico de las sociedades occidentales (D'Ambrosio, 2010).
Planteo que es necesario develar los mecanismos a través de los cuales procesos de marginalización y exclusión tanto de maestros como de estudiantes tienen lugar durante las prácticas de enseñanza y aprendizaje de las matemáticas. Es fundamental entender las formas por las que el poder funciona en la escuela para producir tal marginalización y exclusión. En el caso de las inequidades raciales en la educación matemática, señalo la importancia de visibilizar las ideologías raciales o frameworks (Bonilla–Silva, 2010) en relación con las prácticas e interacciones que le dan forma a las experiencias escolares de los estudiantes negros. Esto es particularmente importante para la comunidad investigativa y para la sociedad en Colombia, dada la escasez de trabajos que aborden estas problemáticas.
Metodología
Por la naturaleza del estudio, que se ubica en la intersección de las prácticas de enseñanza de las matemáticas en sus relaciones con problemáticas de poder, para la recolección y análisis de los datos se utilizó un enfoque cualitativo y herramientas y técnicas de esta tradición investigativa (Creswell, 2007). Dicho enfoque permitió documentar y analizar las ideologías raciales en los discursos que los maestros utilizan para justificar, explicar y naturalizar el desempeño matemático de sus estudiantes negros. Fue posible, además, observar de primera mano y analizar las prácticas de enseñanza de las matemáticas y las interacciones que tienen lugar en los salones de clase con presencia de estudiantes negros.
En particular, el método comparativo permitió establecer similitudes y diferencias entre los discursos y las prácticas de Diana, Juan y Pedro, tres maestros cuyas escuelas se ubican en tres contextos sociales, económicos y culturales distintos en la ciudad de Cali. Aunque los estudios comparativos generalmente se utilizan para determinar la forma en que un fenómeno social dado es influenciado y configurado por contextos culturales, lo que se denomina cross–cultural research, (Mills, van de Bunt, y de Bruijn, 2006), diferentes investigadores (Bernard, 2006; Ragin, 2006) señalan su utilidad para adelantar estudios en contextos urbanos, como es el caso de este estudio. La diversidad en la composición racial, social, cultural y económica de las escuelas seleccionadas hace pertinente el uso de este método de investigación.
Contexto del estudio
La selección de las escuelas y los maestros implicó un proceso no probabilístico. En primer lugar, las escuelas fueron seleccionadas teniendo en cuenta la composición racial y económica de las comunas en las cuales estaban ubicadas. Los maestros fueron escogidos teniendo en cuenta su interés en participar, su formación matemática y los años de experiencia enseñando esta disciplina y en particular álgebra. El control de esta variable era fundamental para evitar que diferencias en las prácticas de enseñanza pudiesen vincularse a diferencias en los años de experiencia enseñando matemáticas.
Tres instituciones educativas fueron seleccionadas para hacer parte del estudio, dos oficiales "La Esperanza" y "La Primavera", y una privada: el "Colegio San Juan".1 Esta última institución se seleccionó con el objetivo de contar con estudiantes de estratos 5 y 6, los cuales generalmente no atienden el sistema educativo público. "La Esperanza" se encuentra ubicada en el distrito de Aguablanca en una comuna en donde el 51% de sus habitantes se reconocen como afros, afrocolombianos o negros. Este promedio, que está por encima del de la ciudad, hace que la comuna sea una de las que cuenta con mayor presencia de población negra viviendo además en condiciones de pobreza. La comuna experimenta situaciones de violencia, inseguridad y en general de abandono estatal muy similares al resto de comunas que conforman el distrito.
Aunque "La Primavera" y el "Colegio San Juan" se encuentran ubicadas en la misma comuna, son atendidas por poblaciones totalmente distintas. La comuna es una de las más tradicionales de Cali, habitada principalmente por las élites políticas y económicas de la ciudad (Urrea, 2012). A "La Primavera" asisten estudiantes de los sectores más pobres de la comuna cuyos habitantes trabajan generalmente como empleados de los habitantes más pudientes de dicha comuna. La mayoría de sus estudiantes provienen de hogares de estratos 1, 2 y 3 y sólo un 10% se auto–reconocen como afros, afrocolombianos o negros. Por su parte, al "San Juan" asisten estudiantes provenientes de los estratos 5 y 6. Como una expresión de la intersección de raza y clase en la ciudad, el porcentaje de estudiantes negros es de aproximadamente el 2% en este colegio; ninguno de ellos cursaba grado octavo en el momento del estudio.
Participantes
Maestros: El estudio comprendió la observación de las clases de Diana, Juan y Pedro, quienes enseñaban en grado octavo al momento de la recolección de los datos. Diana es ingeniera de formación aunque ha dedicado 13 años de su vida profesional a enseñar matemáticas a nivel universitario. Tiene además una especialización en pedagogía de una universidad de la ciudad. Hace tres años llegó a la institución educativa "La Esperanza" y desde entonces ha enseñado álgebra en el grado octavo. Juan es licenciado en matemáticas y desde hace más de 30 años ha estado vinculado a la docencia, aunque solo ha enseñado matemáticas en el bachillerato durante los últimos cinco, todos en grado octavo. Pedro también tiene un título en matemáticas y física. Empezó su carrera como docente hace 30 años en la básica primaria. Desde hace 13 años enseña matemáticas en el "Colegio San Juan" en las mañanas, mientras que en las tardes lo hace en una institución educativa pública de la ciudad. Aunque siempre había enseñado matemáticas en los grados superiores, desde hace tres años y por disposiciones de las directivas del colegio ha enseñado álgebra en los grados octavo. Los tres maestros se auto–reconocen como mestizos y de clase media. La tabla 3 resume la composición racial y económica de sus salones.
Estudiantes: En promedio cada grupo observado constaba de 33 estudiantes. De cada grupo, cuatro estudiantes fueron seleccionados para utilizar un dispositivo móvil de grabación que capturara de manera más detallada sus interacciones y actos de posicionamiento en clase. Los estudiantes fueron seleccionados teniendo en cuenta su identificación racial, así como su disposición para participar en el estudio. La tabla 4 resume las características de los estudiantes seleccionados.
Recolección de los datos
Para la recolección de los datos se utilizaron cuatro técnicas: observación participante, filmación de las clases, entrevistas con estudiantes y maestros, y recolección de documentos curriculares y de enseñanza diseñados y/o utilizados por los maestros. Asistí a las tres instituciones participantes durante cuatro semanas durante el año lectivo 2013; lo que permitió acceder a sus distintos espacios, documentar diversas dinámicas y rutinas, y observar distintos tipos de interacciones entre estudiantes, maestros y directivos. Todas las observaciones fueron recopiladas en un diario de campo para ser analizadas posteriormente.
Además filmé ocho sesiones de clase de cada maestro, utilizando dos tipos de dispositivos: una cámara que capturaba las dinámicas del salón en general, y cuatro gafas con cámaras instaladas. Investigadores como Pinnow y Chval (2014) señalan la utilidad de este tipo de dispositivos para capturar y analizar los actos de posicionamiento de estudiantes de minorías étnicas y raciales durante los procesos de enseñanza y aprendizaje. En el presente estudio, las gafas fueron utilizadas por cuatro estudiantes en cada grupo durante las clases, lo cual me permitió capturar con mayor detalle las interacciones entre estos estudiantes, sus demás compañeros y los respectivos maestros.
Conduje entrevistas semi–estructuradas a estudiantes y a maestros. En primer lugar, entrevisté a los cuatro estudiantes seleccionados para recoger aspectos de su historia personal y de sus experiencias como estudiantes de matemáticas en las instituciones educativas. En segundo lugar, utilicé este mismo tipo de entrevistas para recolectar información acerca de las experiencias de los maestros en sus instituciones educativas, sus historias y sus expectativas sobre los estudiantes. Finalmente, una vez cada semana y utilizando episodios video grabados de sus clases y previamente seleccionados, entrevisté a los maestros participantes con el propósito de analizar a profundidad diferentes situaciones que tenían lugar en el salón de clase. Los planes de área y de clase, y los dispositivos didácticos como evaluaciones y talleres diseñados por los maestros fueron recolectados para ser analizados.

Dadas las características del estudio y la naturaleza de los datos recolectados, introduje un enfoque interpretativo (Hatch, 2002) para adelantar el análisis. El proceso de análisis comprendió cuatro fases diferentes. En la primera, las transcripciones de las entrevistas fueron cuidadosamente leídas con el propósito de identificar temas potenciales. Luego, la misma actividad fue realizada con los videos usando en ambos casos el software de análisis cualitativo Nvivo 10®. Este proceso se repitió varias veces en aras de refinar dichos temas. En una tercera fase se inició el proceso de identificación de categorías con base en los temas identificados. Los datos fueron entonces organizados de acuerdo con dichas categorías. Durante esta fase realicé una selección conceptual de los datos obtenidos. Finalmente, realicé una caracterización conceptual de las categorías identificadas así como de sus interrelaciones tomando como base la literatura existente al respecto. En el próximo apartado, presento los principales resultados.
Resultados
Los resultados del estudio revelan tres aspectos fundamentales. En primer lugar, el uso persistente por parte de los maestros de las identidades raciales, étnicas y de clase de los estudiantes para explicar, justificar y naturalizar sus experiencias escolares y resultados de aprendizaje en matemáticas. En segundo lugar, el uso de prácticas de enseñanza que obstaculizan el aprendizaje significativo de las matemáticas y se oponen al desarrollo de procesos de pensamiento matemático complejos en las escuelas con mayor presencia de estudiantes negros. Finalmente, los resultados muestran que en estas escuelas los estudiantes negros son posicionados por los maestros como incapaces de aprender matemáticas, en contraste con la forma como son posicionados los estudiantes mestizos. En los próximos párrafos analizo en detalle cada uno de estos resultados.
Ideologías raciales en la clase de matemáticas
El análisis de las narrativas de los maestros participantes en el estudio ilumina las formas en las cuales las identidades de los estudiantes nutren sus discursos. Dichas narrativas expresan además las representaciones que los maestros han construido acerca de sus estudiantes y sobre sus posibilidades de éxito en el aprendizaje de las matemáticas. Así, por ejemplo, durante la primera entrevista con cada uno de los maestros, les pedí que describieran a sus estudiantes del grado octavo observado. Sus respuestas fueron2:
D: Algunos de ellos no se interesan en nada. No les importa educarse.L: ¿Podría explicar mejor su respuesta?
D: Desde que llegué aquí, he enseñado en los grados octavo y algunas veces en séptimo.
Y ellos son niños que, es decir, no les interesa el estudio. Yo creo que ellos no visualizan muy bien que para tener un buen futuro necesitan estudiar. Así que uno tiene que empujarlos mucho. (Entrevista, Agosto 20).
Coincidiendo con la representación de Diana sobre sus estudiantes, Juan ha construido la siguiente representación sobre los estudiantes:
J: El grupo, pues, en términos generales, hoy en día lo veo mejor que antes y ha obtenido mejores resultados; pienso que algunos son muy capaces, unos pocos. Hay otros niños que sí traen unos esquemas mentales matemáticos muy deficientes desde el pasado. (Entrevista, Agosto 27).
Pedro, por su parte, describe a sus estudiantes de la siguiente manera:
P: A ellos les encanta el álgebra. Les encantan las matemáticas. A la mayoría de ellos les va muy bien en matemáticas. Aunque yo sólo les he hecho algunos test cortos, los he visto trabajando, haciendo preguntas, y resolviendo ejercicios en sus cuadernos. Ellos siempre quieren resolver problemas en el tablero. Los estudiantes en este colegio siempre escogen carreras con un fuerte contenido matemático. Setenta por ciento de nuestros egresados escoge ingenierías, administración, ciencias, etc. Sólo unos pocos escogen humanidades. (Entrevista, Septiembre 5).
Los primeros discursos de Diana y Juan expresan representaciones negativas de sus estudiantes y comunican las bajas expectativas que tienen acerca de que ellos aprendan matemáticas. De acuerdo con estas representaciones, los estudiantes son desinteresados, tienen dificultades para el aprendizaje y no valoran la educación ni la ven como un medio para mejorar sus condiciones de vida. En contraste, Pedro representa a sus estudiantes como motivados, ansiosos de aprender y anticipa su éxito en el aprendizaje de las matemáticas. Pareciera que, para Pedro, sus estudiantes cuentan no sólo con la motivación sino además con las disposiciones para aprender matemáticas.
En el caso de Diana, sus bajas expectativas son justificadas por lo que ella considera una falta de visión sobre el futuro en sus estudiantes, ya que de acuerdo con su percepción, sus ambiciones se limitan a pertenecer a pandillas y en el caso de las niñas, a ser madres. Esta representación emerge en la siguiente narrativa:
D: Ellos piensan: "Yo no necesito estudiar mucho porque para eso [ser un pandillero], no necesito estudiar". Las niñas se embarazan muy rápido, entonces ellos desertan [de la escuela]. Yo creo que ellos no ven la educación como una manera de mejorar sus vidas. (Entrevista, Agosto 20).
En esta misma línea discursiva, Diana considera que para triunfar los estudiantes necesitan esforzarse, pero que esta cualidad, la del trabajo duro, se encuentra ausente entre sus estudiantes:
D: Ellos no son conscientes. Creen que las cosas son simples, fáciles. Ellos no creen en aquello que nosotros les mostramos, porque hay dificultades, y para alcanzar los objetivos [de terminar el bachillerato e ir a la universidad] necesitan trabajar duro. Yo pienso que ellos no creen en el trabajo duro y la realidad los golpea cuando obtienen malas notas en las pruebas Saber 11. (Entrevista, Septiembre 3).
En este mismo sentido, Juan considera que:
J: Para ellos como que el norte es trasegar por donde quiera, pasarla chévere, entonces uno les pregunta: ¿Que les gustaría? ¿Qué viene usted a hacer aquí? [Y ellos responden] "A pasarla chévere." Y, bueno, ¿qué es pasarla chévere, para usted? [Y ellos responden] "No, pues a tener amigos, charlar." (Entrevista, Agosto 27).
En contraste, la narrativa de Pedro muestra a unos estudiantes ambiciosos, altamente motivados y con un sentido muy claro de las razones para estar en la escuela. Los estudiantes del salón de Pedro valoran la educación y parecen aprovechar el tiempo de clase para aprender, tal y como el maestro lo comunica en la siguiente narrativa:
P: [Los estudiantes en mi salón] hacen preguntas constantemente sobre los temas que uno está enseñando, participan y entienden lo que uno está explicando. Ellos tienen una idea clara de lo que uno está haciendo en clase. Es decir, ellos muestran interés, lo llaman a uno todo el tiempo: "Profesor, este [ejercicio] está bueno, cierto?" entonces uno ve lo que ellos están haciendo. (Entrevista, Septiembre 21).
En las narrativas de Diana y Juan los estudiantes son representados como carentes de valores como el trabajo duro y la ambición, los cuales, desde su perspectiva, son necesarios para triunfar en la institución educativa. Lo anterior en abierto contraste con las representaciones construidas por Pedro, quien describe a sus estudiantes como altamente motivados y con las disposiciones necesarias para triunfar, incluso más allá del mundo del colegio: en la universidad y en la vida social.
Al indagar por las razones de la aparente falta de interés de sus estudiantes y las bajas expectativas en su educación, Diana y Juan apelan no sólo a las identidades raciales sino también a las de clase para anticipar y explicar el fracaso escolar en matemáticas de sus estudiantes. El análisis de estos discursos revela la forma como las ideologías raciales se expresan en dos frameworks que denomino: déficit cultural y déficit social. Como veremos, estos frameworks interactúan para configurar las experiencias de aprendizaje de las matemáticas de los estudiantes negros en el estudio.
Framework del déficit cultural
En los discursos relacionados con el déficit cultural se representa a los estudiantes negros como culturalmente inferiores. En el marco de este racismo cultural (Bonilla–Silva, 2010) o etnicismo (Van Dijk, 2004) se considera a los estudiantes negros como provenientes de culturas que no aprecian los valores predominantes en la cultura occidental, que son necesarios para triunfar en la escuela, en general, y en el aprendizaje de las matemáticas, en particular.
De acuerdo con estas narrativas, en las culturas de las comunidades negras existe una sobrevaloración de los sentidos sobre la mente, del trabajo manual sobre el intelectual, del trabajo físico sobre el mental, y del cuerpo sobre la mente. Un ejemplo de esta narrativa es expresado por Juan en la siguiente conversación sostenida durante una de las entrevistas:
L: ¿Cómo cree que las diferencias culturales que usted menciona influyen en el aprendizaje del álgebra?J: Primero, la ausencia en esos lugares de un tipo de educación que ayude al desarrollo del pensamiento matemático. Segundo, hay más interés por otros tipos de actividades que no son necesariamente cognitivas. Puede haber poco interés en desarrollar [pensamiento matemático] en esas comunidades. ¿Y qué tal que el proyecto educativo institucional no esté centrado en ir a una universidad?, que tal que algunos dijeran "el PEI de nuestra idiosincrasia va ser cultivar la tierra y desarrollarnos por ahí"; o "nuestro PEI está orientado hacia las manualidades", donde las matemáticas son tocadas muy tangencialmente; eso puede ser; o de pronto piensan: "y no, es que nosotros tenemos todo el biotipo para ser deportistas." Hay que aconsejarlos. Sí, pienso que [las diferencias culturales] pueden afectar en un momento dado [el aprendizaje del álgebra] y en un buen porcentaje también, sin decir que a todos (Entrevista, Septiembre 4).
En un movimiento discursivo característico de su narrativa (Van Dijk, 1987), Juan menciona algunas excepciones a esta representación dominante de la cultura negra. Sin lugar a dudas, al introducir estas excepciones, Juan confirma la fuerza de la ideología del déficit cultural en las representaciones construidas sobre los estudiantes negros, tal y como se evidencia en la siguiente narrativa:
J: Sí, las diferencias culturales deben afectar [el aprendizaje del álgebra]. Yo entendería, sin decir de que por esa razón todos tengan que entrar en lo mismo, porque yo me encontré con compañeros de estudio de raza negra, inclusive, que supuestamente son muy dedicados al jolgorio, yo estudié en Quibdó, y eran muchachos muy brillantes; no necesariamente les gustaba demasiado el jolgorio, la danza y todo eso. También me encontré con muchachos de raza indígena en la universidad, el muchacho Jair muy muy brillante, con los procesos bien y tal, entonces: decir que es determinante para todos no, pero sí podría estar afectando a su mayoría. (Entrevista, Septiembre 4).
Un ejemplo adicional de la ideología del déficit cultural se encuentra en las narrativas de Diana, quien apela a diferencias culturales para justificar el fracaso escolar en matemáticas de los estudiantes negros. En sus narrativas es posible apreciar la forma como las características que asocia a la cultura negra son consideras patológicas: como enfermedades que deben ser tratadas por especialistas, para garantizar que los estudiantes puedan obtener mejores resultados de aprendizaje.
L: ¿Usted considera que los estudiantes negros en su salón necesitan algún tipo de apoyo adicional para aprender matemáticas?D: No sólo para aprender matemáticas. Yo creo que ellos necesitan apoyo para aprender cualquier cosa. A ellos no les gusta leer y leer es fundamental para [el aprendizaje de] cualquier área en la escuela; a ellos no les gusta leer, y por eso ellos no entienden los diferentes conceptos, las bases de las distintas áreas. Y ellos tampoco tienen la cultura de [cumplir con] las tareas.
L: ¿Qué tipo de apoyo necesitarían? D: Yo creo que sicológico y también terapia ocupacional. L: ¿Por qué?
D: Porque así ellos pueden extraer sus problemas. Esto es algo que los profesores no podemos hacer, no tenemos la formación para ello. Nosotros estamos preparados para enseñar, pero no sabemos cómo enfrentar las dificultades de estos estudiantes. Y ellos tienen además problemas de desplazamiento forzado, drogadicción, pandillas, todo ese tipo de cosas que a veces uno no sabe cómo lidiar con todo eso. Y yo me digo: "¡Dios! ¿qué más debería hacer? ¿Qué más puedo hacer?" Además, nosotros no tenemos tiempo para esto. (Entrevista, Septiembre 17).
La representación dominante de las matemáticas en el mundo occidental excluye epistemologías y prácticas de las comunidades negras (Ernest, 1991) en lo que podríamos considerar una tradición selectiva (Williams, 1981). De acuerdo con Powell (2002), el carácter peyorativo con el que se representa a las culturas de las comunidades negras en el mundo ha resultado en la exclusión sistemática de los currículos de prácticas matemáticas y modos de conocer asociados a dichas culturas. Esta exclusión e invisibilización curricular parece dejar sin muchas oportunidades de aprendizaje de esta disciplina a los estudiantes negros, quienes no ven su cultura representada en los currículos escolares.
La ideología del déficit cultural, tal y como emerge de las narrativas de Diana y Juan, expresa representaciones dominantes según las cuales sus estudiantes negros no cuentan con las habilidades y disposiciones para aprender matemáticas. Ellos aprecian otros modos de conocer y de vivir, que aunque importantes no garantizan el éxito escolar en matemáticas, por tanto no son valiosas. Es así como, por ejemplo, la escritura y la lectura se imponen sobre la oralidad, la cual no es reconocida por Diana como una forma válida de conocimiento en la escuela.
Esto es particularmente importante para el análisis de los resultados de aprendizaje del álgebra. Con base en la ideología del déficit cultural, las posibilidades de éxito en el aprendizaje de esta disciplina serían menores entre estudiantes de comunidades negras con una fuerte tradición oral, en tanto que el álgebra se presenta como un sistema simbólico que apela fundamentalmente a la escritura y la manipulación sintáctica de símbolos escritos. Una ideología del déficit cultural contribuye a naturalizar el fracaso en el aprendizaje del álgebra entre estudiantes negros.
Además de las bajas expectativas en relación con el aprendizaje del álgebra, expresadas por Diana y Juan en relación con sus estudiantes negros, estos son representados como incapaces de aprender matemáticas debido a sus condiciones de pobreza. Es la ideología del déficit social que asocia a los estudiantes negros con la ausencia de valores, disposiciones y actitudes propios que la clase media representa como necesarios para triunfar en el mundo social (McNamee y Miller, 2004). Unos primeros indicios de la existencia de dicha ideología se aprecia en las narrativas de Diana y Juan, al asociar a sus estudiantes pobres con falta de ambición, visión de futuro y valoración de la educación como un medio de movilidad social. Veamos en detalle las características de esta ideología.
Perspectiva del déficit social
La ideología del déficit social comunica estereotipos dominantes sobre la pobreza y los pobres. En estos discursos emerge de manera importante la estrecha relación entre raza y clase, asociándose los estudiantes negros a la pobreza. En términos generales, en el contexto de estos discursos se expresan estereotipos que los representan como anti– trabajo, anti–escuela, anti–familia y por tanto como incapaces de triunfar en el mundo social (McNamee y Miller, 2004). Es posible apreciar en las narrativas de los maestros participantes la presencia de estas representaciones, en las cuales ciertos valores y normas como el trabajo duro, la ambición, la perseverancia, la armonía familiar y el mérito individual se introducen como condiciones para aprender matemáticas y alcanzar altos niveles de desempeño en esta disciplina. En este sentido, los maestros apelan a valores, disposiciones y actitudes que reflejan mejor la cultura de la clase media (Giroux, 1981) y que refuerzan estereotipos y representaciones negativas de los estudiantes pobres. Los valores representativos de las clases medias y altas (Rist, 1970; Zevenbergen y Niesche, 2008) son considerados ausentes entre los estudiantes pobres; por ejemplo, Juan considera la pobreza como un factor que impide el buen desempeño en la escuela:
J: La pobreza es un factor que determina lo que los estudiantes hacen aquí [en la escuela].La pobreza contribuye a la falta de motivación para venir a estudiar; los estudiantes [pobres] no vienen con el deseo de decir: "yo vengo [a la escuela] a aprender porque necesito este conocimiento para progresar, porque quiero terminar el bachillerato, porque un día voy a ir a la universidad y me veo como un profesional."
L: ¿O sea que para usted la pobreza es un factor que determina lo que los estudiantes hacen en clase?
J: En realidad, sí. La mayoría de las veces es atípico encontrar un estudiante con grandes limitaciones económicas y que le vaya bien en la escuela. Aunque yo he visto unos pocos y con buena disciplina. (Entrevista, Septiembre 4).
Diana, por su parte, apela al contexto social y económico del distrito de Aguablanca en el que viven los estudiantes para justificar el fracaso escolar:
D: Ella [otra maestra] siempre me ha dicho que los estudiantes acá son diferentes. O sea, el ambiente en el que viven aquí es diferente, por las condiciones del distrito, y no es posible aquí hacer el mismo trabajo que uno podría hacer en otra escuela [fuera del distrito].L: ¿Por qué crees que esta idea es tan extendida?
D: ¿Por el contexto en el que ellos viven? La gente lo ha generalizado de esa manera. Es decir, las áreas donde vive la gente vulnerable, con pocas oportunidades de empleo, uno las relaciona con gente que no tiene ambiciones, que no quiere alcanzar nada en la vida, no quieren algo mejor o no pueden, no sé. Yo sé, por mis colegas que dicen que el distrito tiene un ambiente especial, es una sociedad diferente: [los estudiantes] traen un mundo de problemas desde la casa; particularmente, Emma quien ha trabajado acá por 23 años [me ha dicho eso]. (Entrevista, Septiembre 3).
Es importante resaltar que en el caso particular de Diana, las representaciones construidas acerca de sus estudiantes provienen de narrativas construidas por otros maestros y de imágenes que circulan en la sociedad, lo cual confirma su carácter ideológico y prejuicioso. Es claro que Diana también se considera social y moralmente mejor que sus estudiantes y se presenta como un modelo para ellos, tal y como lo afirma en la siguiente narrativa:
D: Mi principal objetivo es darle a los estudiantes mensajes positivos sobre la vida. Más que enseñarles álgebra, mi objetivo es mostrarles un buen ejemplo e inculcarles valores, ese tipo de cosas. Eso es más importante para ellos. (Entrevista, Septiembre 3).
En contraste con las narrativas de Diana y Juan, Pedro no construye las representaciones de sus estudiantes sobre sus identidades raciales o de clase. En términos muy generales, los resultados de aprendizaje de las matemáticas no dependen de dichas identidades sino de las dinámicas propias de la institución educativa. Así, por ejemplo, Pedro afirma que:
P: Todos los estudiantes en mi clase tienen el mismo chance de pasar. A ellos les gusta el álgebra y yo creo que se la gozan y quieren aprender. He visto algunos pocos que pueden tener problemas, pero [su futuro desempeño] depende de usted como profesor. Si ellos fallan es por la falta de esfuerzo de los maestros. El año pasado, había tres grados séptimos. Este año hay sólo dos octavos porque 28 estudiantes no pasaron. Ese es un gran problema. Yo no puedo creer que usted tenga 28 estudiantes malos en un grupo. Yo creo que algo tuvo que haber pasado el año pasado.L: ¿Qué cree usted que pasó?
P: Los métodos de enseñanza, los métodos de enseñanza, Luz, porque en un grupo de estudiantes hay dos o tres que aprenden más rápido que el resto. Pero si uno se va con los más rápidos, te vas a tirar el resto. Yo supongo que eso pasó el año pasado. (Entrevista, Septiembre 5).
Es evidente que Pedro asigna la responsabilidad del éxito o fracaso escolar de los estudiantes a los maestros y a sus métodos de enseñanza. El silencio acerca de las identidades raciales y de clase como fuentes de explicación del desempeño matemático de los estudiantes podría explicarse por el hecho de que los estudiantes de Pedro son más cercanos a las representaciones construidas acerca de los estudiantes exitosos. Ellos son clase media y mestizos, y por tanto, sus valores se alinean a las actitudes y comportamientos requeridos para el éxito académico (Giroux, 1981).
Así pues, la intersección de raza y clase constituye una doble amenaza para el aprendizaje de las matemáticas en los estudiantes de los salones de Diana y Juan. Por su doble condición de negros y pobres estos estudiantes son representados como incapaces de aprender matemáticas; por tanto, sus experiencias escolares así como sus resultados de aprendizaje van a estar mediadas por estas condiciones. Las ideologías utilizadas por Diana y Juan para anticipar, justificar, explicar y finalmente naturalizar el fracaso escolar en matemáticas de los estudiantes negros, evidentemente los libera de responsabilidad ante el fracaso. Recurrir a estas ideologías les permite, a Diana y Juan, presentarse como actores lejanos y neutrales en la configuración del bajo rendimiento académico de los estudiantes, el cual se debe a las deficiencias culturales y de clase de sus estudiantes.
Van Dijk (2004) señala el papel de estos discursos esencialistas en la comunicación, reproducción y en la formación del racismo en la sociedad, y en este caso en particular, en la escuela. De hecho, las narrativas de Diana y Juan con la fuerte carga ideológica que comunican son, de acuerdo con Van Dijk (1992), prácticas de discriminación racial. Tenemos pues en la enunciación de tales discursos una de las principales manifestaciones de racismo en las instituciones participantes del estudio.
Es importante anotar que estos resultados coinciden con los de diferentes estudios que señalan las relaciones estrechas entre las expectativas de los maestros acerca del aprendizaje de las matemáticas y las identidades raciales y de clase de los estudiantes (Boaler, Altendorff, y Kent, 2011; Frankestein, 1995; Hoadley, 2007; Lim, 2008; Ogbu, 1988; Reyes y Stanic, 1988). Estos estudios confirman que las representaciones construidas por los maestros acerca de sus estudiantes y las anticipaciones acerca del aprendizaje de las matemáticas recogen y expresan compresiones del mundo social, de los individuos y de prácticas sociales que trascienden la escuela. Para una mejor comprensión de las experiencias de los estudiantes socialmente marginalizados es fundamental atender las dimensiones políticas, económicas, sociales e históricas de la sociedad en las cuales se construyen los sistemas educativos.
Aunque fundamentales, las ideologías raciales no son suficientes para explicar los bajos resultados de aprendizaje de los estudiantes negros en el sistema educativo colombiano. En concordancia con la perspectiva teórica asumida, señalo y exploro la estrecha relación entre ideologías raciales y prácticas de enseñanza de las matemáticas. En este sentido, los resultados de este estudio indican la forma como las ideologías raciales configuran y determinan las prácticas de enseñanza de las matemáticas.
Como veremos en el siguiente apartado, los maestros toman decisiones didácticas que determinan sus experiencias de aprendizaje las matemáticas con base en las representaciones de sus estudiantes. Así, los estudiantes negros son expuestos a prácticas de enseñanza descontextualizadas y que difícilmente les permitirá construir conocimiento matemático significativo o desarrollar procesos de pensamiento matemático complejo.
Prácticas de enseñanza e interacciones en la clase de matemáticas
Los resultados del estudio evidencian el uso sistemático de prácticas de enseñanza y la naturaleza de las interacciones en el salón de clase que podrían contribuir a explicar los bajos desempeños en matemáticas de los estudiantes negros en Colombia. Así, las prácticas de enseñanza que predominan en los salones de Diana y Juan se caracterizan en primer lugar por su énfasis en el aprendizaje de procedimientos memorísticos en los cuales no se requiere desarrollar procesos de pensamiento complejos como el razonamiento, la resolución de problemas o la argumentación. En segundo lugar, Diana y Juan introducen estrategias para aparentemente ayudar a sus estudiantes a construir significados para los objetos, conceptos y procedimientos algebraicos, pero que contribuyen a obscurecer tanto el significado como el uso con sentido de dichos objetos. Finalmente, las interacciones en el salón de clase posicionan a los estudiantes como incapaces de adelantar procesos de pensamiento matemático complejo.
Por ser un elemento fundamental en la configuración del bajo desempeño de los estudiantes negros, voy a comparar las estrategias utilizadas por Diana y Pedro para enseñar por primera vez a sus estudiantes uno de los conceptos más importantes en las matemáticas secundarias: la variable. Una de las estrategias sistemáticamente utilizada por Diana consiste en introducir nociones algebraicas usando contextos de la vida cotidiana aparentemente cercanos a las experiencias de los estudiantes. Así, por ejemplo, en la clase en que introduce el concepto de variable, Diana procede de la siguiente manera:
(Diana dibuja un conjunto de cinco corazones en el tablero)D: Observemos el tablero. Acá tenemos un conjunto, y como ustedes siempre están enamorados, dibujemos un conjunto de cinco corazones. ¿De qué es este conjunto?
E: ¡Corazones!
(Diana escribe en el tablero "corazones").
D: ¿Cuántos corazones vemos aquí?
E: ¡Cinco!
D: Tenemos cinco corazones, bien. Sin embargo, escribir "cinco corazones" nos toma mucho tiempo, así que podemos expresarlo con el número cinco y un corazoncito (Diana escribe el número cinco y dibuja un corazón a su lado). ¿Pero qué pasaría si en vez de un corazón tuviéramos mariposas? Nos tomaría mucho tiempo dibujar mariposas, ¿cierto? Pues nosotros podemos reemplazar el corazón con una letra. ¿Cuál letra?
E: ¡la c!, ¡la m!
D: Ok. Usemos la c. ¿Cuál es el significado de la c?
E: ¡Corazones! D: ¡Muy bien!, corazones. Miren, esto es el álgebra. Es tan simple como esto. Las letras van a reemplazar objetos conocidos y desconocidos, cosas que son conocidas o desconocidas. Observemos que después de tener cinco corazones, pasamos a tener 5c en donde la letra c representa un objeto llamado "corazón". (Clase, Agosto 22).
En este episodio, Diana identifica la variable con un objeto de la vida real, y en este sentido, la variable es el objeto representado por la letra y no una entidad matemática que varía bajo ciertas condiciones. Claramente, la variable se ha transformado en un objeto material de la cotidianidad que acompaña a los coeficientes. La variable emerge como la abreviación del nombre de un objeto de la vida cotidiana o como una etiqueta (Philipp, 1992). En este proceso, las relaciones matemáticas que se representan en las expresiones algebraicas han desaparecido completamente. Por ejemplo, en la explicación de Diana, "5c" no representa una relación aditiva o multiplicativa sino una abreviación para la expresión "cinco corazones". Además de ignorar la relación matemática representada por la expresión algebraica, el contexto utilizado por Diana difícilmente le ayudaría a los estudiantes a comprender la noción de variable, el cual es matemáticamente irrelevante y parece ser introducido para llamar la atención de los estudiantes y como herramienta nemotécnica, para ayudarles a recordar cómo usar variables.
El tratamiento dado a la variable y el uso de contextos aparentemente familiares para los estudiantes para significar los objetos algebraicos es una práctica recurrente en las clases de Diana, tal y como puede observarse en el siguiente episodio de clase.
(Diana explica a los estudiantes como simplificar la expresión 7a – 9b + 6a – 4b)D: Recordemos lo que hicimos en la última clase. Vimos lo que eran términos semejantes, o sea, los que tienen la misma letra y el mismo exponente. Este tiene la letra a (señalando 7a) y este también tiene la letra a (señalando 6a). Entonces, yo puedo juntarlos y me da una sola respuesta. Siete más seis es trece y le escribo la letra a. Ahora, tengo menos nueve y tengo otra que también tiene [la letra] b que es menos cuatro b. Ok. Recuerden que el signo menos es como dinero que debemos. Entonces yo debo nueve y podemos suponer que –9b–4b quiere decir que debo nueve bombones y cuatro bombones, entonces ¿cuantos bombones debo? Trece. Y esa es la respuesta final. 13b (Clase, Agosto 26).
Este episodio de clase confirma el despojo del significado matemático de la noción de variable, la cual sólo emerge como un accesorio después que se ha operado con los números y en este sentido, ella sólo acompaña o está al lado (físico) de los coeficientes. Antes que construir significado para las operaciones algebraicas con base en las propiedades matemáticas de los sistemas numéricos, Diana introduce un contexto de "deber–tener" que le ayude a los estudiantes a memorizar el procedimiento, pero que obscurece las relaciones matemáticas involucradas. En este sentido, la comprensión significativa de los procedimientos algebraicos es reemplazada por la memorización de pasos y estrategias para llevarlos a cabo y la variable es nuevamente tratada como un objeto de la vida real, como un accesorio que acompaña a los coeficientes. Las relaciones, objetos y procedimientos algebraicos han quedado completamente desdibujados para los estudiantes en la clase de Diana.
Un ejemplo de la forma como las ideologías raciales configuran las prácticas de enseñanza en la clase de Diana, emerge en sus justificaciones acerca de la naturaleza de las estrategias que utiliza para contribuir a la construcción de conocimiento algebraico por parte de sus estudiantes. Diana apela a la percibida falta de habilidades y aptitudes de sus estudiantes para aprender matemáticas para justificar el uso de una serie de estrategias que como hemos visto desvirtúan el poder y la pertinencia del álgebra. Lo anterior es claro en la siguiente narrativa:
D: Yo trato de enseñar de la manera más simple, o sea, trato de hacerlo lo más sencillo posible para que los estudiantes puedan aprender. Y es realmente duro que ellos entiendan, me toca esforzarme mucho.L: ¿Cómo lo hace?
D: Yo trato de explicar claramente; cuando ellos no entienden, me gusta que me pregunten, y yo les repito en diferentes formas, les repito en las formas más simples. Yo trato de usar un vocabulario muy simple para que ellos entiendan. Y también trato de verificar que cada uno ha entendido revisando los cuadernos. (Entrevista, Agosto 20).
En contraste, Pedro utiliza estrategias que la investigación ha demostrado como potentes para la enseñanza del álgebra en grado octavo. Durante las clases observadas, Pedro siempre introdujo un problema verbal o numérico de tal forma que sus estudiantes tuvieran la oportunidad de explorar distintos tipos de propiedades y utilizar el lenguaje algebraico para representar dichas propiedades. En la clase en la que introdujo la noción de variable, Pedro propuso una tarea de generalización pertinente para su objetivo:
P: Hoy vamos a comenzar a usar variables. Escriban por favor el siguiente problema. Tómese su tiempo para resolverlo. Encuentre tres números consecutivos y súmelos. Repita este procedimiento con cinco grupos de tres números consecutivos. Observe todas sus respuestas y escriba lo que observa. ¿Ve algún patrón? ¿Ve alguna regla o regularidad? ¿Qué relación existe entre los tres números consecutivos y la suma? ¿Cómo describiría dicha relación? Tómese su tiempo. Escriba sus respuestas y las revisaremos más adelante. (Clase, Septiembre 6).
Pedro no define la noción de variable. En su lugar, utiliza el tiempo de la clase para que los estudiantes resuelvan la actividad explorando las relaciones entre las variables involucradas en el problema. La solución requiere no sólo identificar patrones y regularidades, actividades éstas consideradas como fundamentales para el aprendizaje del álgebra (Mason, 1996), sino además explorar un sistema de representación para expresar las respuestas. Así, los estudiantes de Pedro tendrán más oportunidades de construir significado matemático correcto y pertinente para la noción de variable a partir de estas experiencias de clase. Adicionalmente, Pedro demanda que sus estudiantes observen, describan y en general razonen sus respuestas. El maestro constantemente invita a sus estudiantes a explicar sus ideas, tal y como el siguiente episodio demuestra:
P: ¿Qué observan? ¿Encontraron alguna regla? ¿Qué patrón pueden deducir?E: ¡Yo, profe, yo! Tengo tres números consecutivos, ¿cierto? Pues siempre el número del medio multiplicado por tres me da la suma.
P: Ok, ok. Todos pongan atención a lo que el compañero está diciendo. Él encontró algo interesante. ¿Podrías repetirlo por favor?
E: La suma es el resultado de multiplicar el número del medio por tres.
P: ¿Están de acuerdo con este resultado? ¿Podrías explicar en el tablero cómo encontraste la respuesta? (Clase, Septiembre 6).
El episodio anterior nos revela que, además de la naturaleza de las estrategias utilizadas por Diana y Pedro para contribuir a que los estudiantes construyan la noción de variable, es importante tener en cuenta la naturaleza de las interacciones entre los estudiantes y los maestros y el nivel de exigencia cognitiva que estos demandan a través de sus preguntas.
En la clase de Diana impera lo que algunos investigadores denominan un modelo de interacción que consiste en que el maestro pregunta y obtiene una respuesta que es finalmente evaluada como correcta o incorrecta. Las preguntas realizadas por Diana a sus estudiantes sólo requieren respuestas cortas, generalmente negativas o positivas, o encontrar la respuesta a una operación sencilla. Ellas no requieren que los estudiantes se involucren en procesos complejos de pensamiento, ni los invita a la exposición de sus ideas y al debate abierto. En contraste, en la clase de Pedro los estudiantes son motivados a argumentar sus respuestas y a exponerlas a la discusión colectiva. En otras palabras, en su clase los estudiantes tienen más posibilidades de desarrollar procesos no sólo de resolución de problemas sino también de argumentación y comunicación fundamentales para el aprendizaje de las matemáticas y para el desarrollo de competencias para la ciudadanía. Los estudiantes de Diana y Pedro son posicionados de manera distinta durante los procesos de construcción del conocimiento algebraico. En clase de Diana, los estudiantes son posicionados como recipientes pasivos de un conocimiento algebraico que resulta ajeno a su experiencia. La baja demanda cognitiva de las preguntas propuestas los posiciona como incapaces de producir matemáticas y de desarrollar pensamiento matemático, con las implicaciones que ello tiene para la construcción de una identidad matemática positiva por estos estudiantes (Nasir, 2002). En la clase de Pedro, los estudiantes no solo desarrollan pensamiento matemático sino que además se posicionan como líderes y sujetos autónomos en la construcción de conocimiento. Su identidad matemática positiva se fortalece a través de estos actos de posicionamiento.
De acuerdo con los resultados de este estudio y en relación con las prácticas de enseñanza, podemos entonces señalar lo siguiente. La estrategia de introducir en el salón de clase contextos de la vida real y aparentemente familiares a los estudiantes es una práctica común en escuelas pobres (Hoadley, 2007). Sin embargo, investigadores como Sfard y Linchevski (1994) y Harel y Kaput (1991) han señalado las dificultades de esta práctica en los procesos de enseñanza del algebra. De acuerdo con estos autores, es necesario que los estudiantes trasciendan el nivel operatorio y accedan al nivel estructural del álgebra. En este nivel, la expresión algebraica es un objeto matemático en sí mismo y se presenta como parte de estructuras matemáticas tales como anillos o campos. Al vincular la noción de variable a contextos cotidianos, o al enfatizar el aprendizaje de las reglas sintácticas del algebra como ocurre en la clase de Diana se obstaculiza el acceso de los estudiantes a este nivel de comprensión de la disciplina y se limita el desarrollo de niveles de pensamiento algebraico que les permitan no sólo avanzar en el sistema educativo sino además y principalmente, pensarse críticamente su ubicación y papel en el mundo social. Al atar el significado de la variable a contextos del mundo real en la forma como sucede en la clase de Diana, el conocimiento algebraico se mantiene en un nivel elemental y matemáticamente nebuloso. Lo anterior en abierto contraste con lo que sucede en la clase de Pedro.
Adicionalmente, distintos investigadores (Stein y Lane, 1996; Turner et. Al., 2002) han llamado la atención sobre la forma como las bajas expectativas de los maestros se traducen en formas de interactuar que posicionan a los estudiantes como incapaces de responder por tareas o por preguntas complejas, tal y como sucede en la clase de Diana. De acuerdo con estos autores, mediante la implementación de estas formas de interacción en clase, los maestros controlan a través de las preguntas el pensamiento y comportamiento de los estudiantes lo cual no sólo limita sus oportunidades de aprendizaje sino además su autonomía. Estos actos de posicionamiento no sólo inciden en el bajo desempeño de los estudiantes en matemáticas sino además en el desarrollo de competencias para participar activamente en la vida democrática de la sociedad. Estas son las formas a través de las cuales las prácticas de enseñanza de las matemáticas contribuyen a la reproducen las inequidades en el logro educativo en el sistema educativo colombiano a lo largo de líneas raciales y de clase.
Conclusiones
Los resultados en este estudio señalan las tensiones raciales existentes al interior de las escuelas participantes y el papel fundamental de ideologías raciales en la justificación, explicación y naturalización del fracaso escolar en matemáticas de los estudiantes negros en la ciudad de Cali. Los resultados son consistentes con estudios que señalan el impacto de las ideologías de los maestros en las experiencias de los estudiantes y en los resultados de aprendizaje (Boaler, Altendorff, y Kent, 2011; Frankestein, 1995; Hoadley, 2007; Ogbu, 1988; Reyes y Stanic, 1988). De hecho, los resultados confirman la existencia de una visión en educación de acuerdo con la cual existe una jerarquía racial de las habilidades matemáticas, en la cual los estudiantes negros se ubican en la parte inferior ya que no cuentan con las disposiciones para aprender exitosamente esta disciplina. Claramente, las identidades raciales de los estudiantes nutren los discursos con los que los maestros justifican los bajos desempeños en matemáticas; las ideologías del déficit cultural y social les permiten a los maestros naturalizar el fracaso en el aprendizaje de las matemáticas y liberarse de su responsabilidad por él.
La intersección de raza y clase constituye una doble amenaza para el aprendizaje del álgebra entre los estudiantes de este estudio. Los estudiantes negros son mayoritarios en los estratos más pobres de la población caleña (Urrea, Viáfara, Ramírez y Botero, 2007); en este sentido, la discriminación y marginalización los afecta doblemente. Por una parte, los estudiantes negros son marginalizados debido a las ideologías del déficit cultural que los representa como incapaces de desarrollar procesos matemáticos complejos. Por otra parte, los estudiantes negros son marginalizados por ideologías del déficit social que los representa como carentes de los valores, actitudes y disposiciones consideradas como necesarios para triunfar en el mundo social. Estos estereotipos emergen como modos de perpetuar la exclusión y marginalización de los estudiantes negros y su sola presencia en los discursos de los maestros despoja a los estudiantes negros de su poder y excluye del sistema los tipos de capital que traen a la escuela con base en sus afiliaciones culturales y sociales (Nasir y Mckinney, 2013).
Los resultados del estudio también revelan los modos en los cuales las ideologías raciales configuran las prácticas de enseñanza e interacciones en la clase de matemáticas. Las representaciones negativas de los estudiantes negros elaboradas por los maestros se traducen en diferencias en las oportunidades de aprendizaje, en las experiencias escolares y en la calidad del conocimiento algebraico al que son expuestos estos estudiantes. Los maestros en el estudio adaptan sus prácticas de enseñanza a las percibidas habilidades de sus estudiantes. Así, los estudiantes negros, al ser considerados incapaces de aprender matemáticas, fueron expuestos a prácticas de enseñanza centradas en el aprendizaje de procedimientos de rutina, en la memorización y en la solución de tareas de baja demanda cognitiva. Esto en contraste con las prácticas utilizadas para enseñar álgebra a los estudiantes ricos y mestizos quienes fueron posicionados como hábiles y capaces para el aprendizaje de esta disciplina. Luego, la relación entre ideologías y prácticas de enseñanza aporta a la comprensión de las experiencias y los resultados de aprendizaje de los estudiantes negros en Colombia.
Es claro que se necesitan más estudios que exploren la forma como la escuela se organiza y estructura a lo largo de líneas raciales para distribuir de manera inequitativa conocimiento y habilidades matemáticas en Colombia. La comunidad colombiana de educadores matemáticos necesita adelantar procesos de investigación en esta línea, de tal forma que contribuyan al alcance del objetivo de la equidad y la justicia social a través de la educación matemática. En este sentido, es necesario repensar las bases teóricas y metodológicas que han orientado la construcción de política educativa pública para las comunidades negras en el país. Se requiere analizar desde los resultados de estudios como el que presento, los procesos de formación de maestros, la etno–educación y las cátedras que se proponen en el sistema educativo como medios para mejorar las condiciones de enseñanza y aprendizaje de la población negra. Mientras no se reconozcan las tensiones raciales existentes al interior de la escuela, la población negra continuará rezagada en el campo educativo.
NOTAS
** El presente artículo de investigación recoge algunos de los principales resultados de la investigación "Colombian teachers' expectations of black and poor students' abilities to learn algebra", adelantada por la autora como requisito para obtener su título doctoral en la Universidad de Missouri, Estados Unidos.
1. Todos los nombres citados son seudónimos.
2. Uso las iniciales de los nombres de los maestros y del mío propio (L) en la presentación de las narrativas.
Referencias
BAIRD, K. (2012). Class in the classroom: The relationship between school resources and math performance among low socioeconomic status students in 19 rich countries. Education Economics, 20(5), 484–509.
BERNARD, H. R. (Rev. ed.) (2006). Research methods in anthropology: Qualitative and quantitative approaches. The U.S.: AltaMira Press.
BERRY III, R. (2008). Access to upper–middle level mathematics: The stories of successful African American middle school boys. Journal for Research in Mathematics Education, 39(5), 464–488.
BOALER, J. (2002). Paying the price for "sugar and spice": Shifting the analytical lens in equity resarch. Mathematics Thinking and Learning, 4(2\3), 127–144.
BOALER, J., ALTENDORFF, L., Y KENT, G. (2011). Mathematics and science inequities in the United Kingdom: When elitism, sexism and culture collide. Oxford Review of Education, 37(4), 457–484.
BONILLA–SILVA, E. (Rev. ed.) (2010). Racism without racists. A color–blind racism y racial inequality in contemporary America. Lanham, MD: Rowman y Littlefield Publishers.
BORMAN, G. D., Y OVERMAN, L. T. (2004). Academic resilience in mathematics among poor and minority students. The Elementary School Journal, 104(3), 177–195.
CRESWELL, J. (2007, 2nd edition). Qualitative inquiry and research design. Choosing among five approaches. Thousand Oaks, CA: Sage Publications.
D'AMBROSIO, U. (2010). Mathematics education and survival with dignity. En H. Alro, O. Ranv, y P. Valero (Eds.), Critical mathematics education: Past, present and future (pp. 51–64), Rotterdam, The Netherlands: Sense Publishers.
DARLING–HAMMOND, L. (2004). The color line in American education. Race, resources, and student achievement. Du Bois Review, 1(2), 213–246.
DIME (2007). Culture, race, power, and mathematics education. En F. Lester (Ed.), Second handbook of research on mathematics teaching and learning (pp.405 –434), The U.S.: Age Publishing.
ERNEST, P. (1991). The philosophy of mathematics education. New York, NY: Falmer Press.
FRANKENSTEIN, M. (1995). Equity in mathematics education: Class in the world outside the class. En W. Secada, E. Fennema, L.B. Adajian (Eds.), New directions for equity in mathematics education (pp. 165–190). Cambridge, MA: Cambridge University Press.
GARCÍA, M., ESPINOSA, J., JIMÉNEZ, F., Y PARRA, J. (2013). Separados y desiguales. Educación y clases sociales en Colombia. Colección DeJusticia. Bogotá, Colombia: Ediciones Antropos.
GIROUX, H. (1981). Ideology, culture, and the process of schooling. Philadelphia, PA: Temple University Press.
HAREL, G., Y KAPUT, J. (1991). The role of conceptual entities and their symbols in building advanced mathematical concepts. En D. Tall (Ed.), Advanced Mathematical Thinking (pp. 82–94). Dordrecht, The Netherlands: Kluwer Academic Publishers.
HATCH, J. A. (2002). Doing qualitative research in education settings. Albany, NY: The State University of New York Press.
HOADLEY, U. (2007). The reproduction of social class inequalities through mathematics pedagogies in South African primarily schools. Journal of Curriculum Studies, 39(6), 679–706
INSTITUTO COLOMBIANO PARA EL FOMENTO DE LA EDUCACIÓN SUPERIOR, ICFES (2009). Saber 5 y 9 2009. Resultados nacionales. Recuperado de http://www.icfes.gov.co/resultados/pruebas–saber–resultados
INSTITUTO COLOMBIANO PARA EL FOMENTO DE LA EDUCACIÓN SUPERIOR, ICFES (2010). Resultados de Colombia en TIMSS 2007. Recuperado de http://www.icfes.gov.co/resultados/pruebas–saber–resultados
LADSON–BILLINGS, G., Y TATE, W. (1995). Towards a critical race theory of education. Teachers College Record, 79(1), 47–68.
LEE, J. (2002). Racial and ethnic achievement gap trends: Reversing the progress toward equity? Educational Researcher, 31(1), 3–12.
LEE, V., SMITH, J., Y CRONINGER, R. (1997). How high school organization influences the equitable distribution of learning in mathematics and science. Sociology of Education, 70(2) 128–150.
LIM, J. (2008). Double jeopardy: The compounding effects of class and race in school mathematics. Equity & Excellence in Education, 41(1), 81–97.
LUBIENSKI, S. (2002). A closer look at black–white mathematics gaps: Intersection of race and SES in NAEP achievement and instructional practices data. The Journal of Negro Education, 71(4), 269–287.
MARTIN, D. (2006). Mathematics learning and participation as racialzed forms of experience: African american parents speak on th struggle for mathematics literacy. Mathematical Thinking and Learning, 8(3), 197–229.
MARTIN, D. (2009). Reseching race in mathematics education. Teachers College, 11(2), 295–338
MASON, J. (1996). Expressing generality and roots of algebra. En N. Bednardz, C. Kieran, y L. Lee (Eds.), Approaches to algebra. Perspectives for research and teaching (pp. 65–86). The Netherlands: Kluwer Academic Publishers.
MCNAMEE, S., Y MILLER, R. (2004). The meritocracy myth. New York, NY: Rowman y Littlefield Publishers.
MILLS, M., VAN DE BUNT, G., Y DE BRUJIN, J. (2006). Comparative research. Persistent problems and promising solutions. International Sociology, 21(5), 619–631.
MOSES, R., Y COBB, C. (2001). Radical equations. Civil rights from Mississippi to the algebra project. Boston, MA: Beacon Press.
NASIR, N. (2002). Identity, goals, and learning. Mathematics in cultural practice. Mathematical Thinking and Learning, 4, 213–247.
NASIR, N. (2007). Identity, goals and learning: The case of basketball mathematics. In N. Nasir y P. Cobb (Eds.), Improving Access to mathematics: Diversity and equity in the classroom (pp. 133– 140). New York, NY: Teachers College Press.
NASIR, N., Y HAND, V. (2006). Exploring sociocultural perspectives on race, culture, and learning. Review of Educational Research, 76(4), 449–475.
NASIR, N. Y MCKINNEY, M. (2013). Power, identity, and mathematical practices outside and inside school. Journal for Research in Mathematics Education, 44(1), 264–287.
OAKES, J. (Rev. ed.) (2005). Keeping track. How schools structure inequality. Binghamton, NY: Yale University Press.
OGBU, J. (1988). Class stratification, racial stratification, and schooling. In L. Weis (Ed.), Class, race, and gender in American education (pp. 163–182), Albany, NY: The SUNY Press.
PARKS, A.M., Y SCHMEICHEL, M. (2012). Obstacles to addressing race and ethnicity in the mathematics education literature. Journal for Research in Mathematics Education, 43(3), 238–252
PINNOW, R. Y CHVAL, K.B. (2014). Positioning ELLs to develop academic, communicative, and social competences in mathematics. En M. Civil y E. Turner (Eds.), The CCSS in mathematics for grades k–8 (pp. 72–95), Arizona, The U.S.: TESOL press
PHILIPP, R. (1992). The many uses of algebraic variables. The Mathematics Teacher, 85(7), 557–562.
POWELL, A. (2002). Etnomathematics and the challenges of racism in mathematics education. En P. Valero y O. Skovsmose (Eds.), Proceedings of the third International MES Conference (pp. 1–15), Copenhagen: Center for Research in Learning Mathematics.
PROGRAMA DE LAS NACIONES UNIDAS PARA EL DESARROLLO, PNUD, (2011). Afrocolombianos: Sus territories y condiciones de vida. Cuaderno del informe de desarrollo humano Colombia 2011. Recuperado de http://www.pnudcolombia.org/indh2011
RAGIN, C. (2006). How to lure analytic social science out of the doldrums: Some lessons from comparative research. International Sociology, 21(5), 633–646.
REYES, L., Y STANIC, G. (1988). Race, sex, socioeconomic status, and mathematics. Journal for Research in Mathematics Education, 19(1), 26–43.
RIEGLE–CRUMB, C., Y GRODOSKY, E. (2010). Racial–ethnic differences at the intersection of math course–taking and achievement. Sociology of Education, 83(3), 248–270.
RIST, R. (1970). Student social class and teacher expectations. The self–fulfilling prophecy in ghetto education. Harvard Educational Review, 40(3), 411–451.
RODRIGUEZ, C., ALFONSO, T., Y CAVELIER, I. (2009). Raza y derechos humanos en Colombia. Informe sobre la discriminación racial y derechos de la población afrocolombiana. Bogotá, Colombia: Ediciones Unidandes.
SFARD, A., Y LINCHEVSKI, L. (1994). The gains and the pitfalls of reification: The case of algebra. Educational Studies in Mathematics, 26(2\3), 191–228.
STEIN, M.K., Y LANE, S. (1996). Instructional tasks and the development of students' capacity to think and reason: An analysis of the relationships between teaching and learning in a reform mathematics project. Educational Research and Evaluation, 2(1), 50–80.
TATE, W. (1997). Race–ethnicity, SES, gender, and language proficient trends in mathematics achievement. Journal for Research in Mathematics Education, 28(6), 652–679.
TURNER, J., MIDGLEY, C., MEYER, D.K., GHEEN, M., ANDERMAN, E., KANG, Y., Y PATRICK, H. (2002). The classroom environment and students' reports of avoidance strategies in mathematics: a multimethod study. Journal of Educational Psychology, 94(1), 88–106.
URREA, F. (2012). Transformaciones sociodemográficas y grupos socio–raciales en Cali a lo largo del siglo XX y comienzos del siglo XXI. Recuperado de http://urosario.edu.co/subsitio/Catedra–de–Estudios–Afrocolombianos/Documentos/14–Fernando–Urrea–Articulo–sobre–Cali–sigloXX.pdf
URREA, F., VIÁFARA, C., RAMÍREZ, H., Y BOTERO, W. (2007). Las desigualdades raciales en Colombia: Un análisis socidemografico de condiciones de vida, pobreza e ingresos para la ciudad de Cali y el departamento del Valle del Cauca (en prensa).
VALOYES, L. (2013). Estudio de la representación del álgebra en los documentos curriculares colombianos. Revista Perspectivas Educativas, 6, 15–32.
VALOYES, L. (2014). Colombian teachers' expectations of black and poor students' abilities to learn algebra. (Unpublished doctoral dissertation). University of Missouri, Columbia, MO.
VAN DIJK, T. (1987). Communicating racism. Ethnic prejudice in thought and talk. Newbury Park, CA: Sage Publications
VAN DIJK, T.(1992). Discourse and the denial of racism. Discourse and Society (3)1, 87–118.
VAN DIJK, T. (2004). Racism and discourse in Spain and Latin America. Philadelphia, PA: John Benjamins Publishing Company.
WALKER, E. (2006). Urban high school students' academic communities and their effects on mathematics success. American Educational Research Journal, 43(1), 43–73.
WILLIAMS, R. (1981). The sociology of culture. Chicago, IL: The University of Chicago Press.
ZEVENBERGEN, R. (2003). Teachers' beliefs about teaching mathematics to students from socially disadvantaged backgrounds: Implications for social justice. En L. Burton (Ed.), Which way social justice in mathematics education? (pp. 133–152). Westport CONN/London: Praeger.
ZEVENBERGEN, R., Y NIESCHE, R. (2008). Equity, Mathematics and Classroom Practice: Developing rich mathematical experiences for disadvantaged students. Australian Primarily Mathematics Classroom, 13(4), 21–27.